Diagramas de cajas
Es un diagrama que muestra datos estadísticos de una variable dada utilizando una caja donde caen la mayoria de los datos y dos brazos cuyas longitudes son propocionales a los valores extremos que toma dicha variable.
Consideremos un ejemplo perteneciente el mundo de la física: se realizaron diez mediciones de la velocidad del sonido y se obtuvieron los siguientes valores:
| Medición # | Velocidad [m/s] |
|---|---|
| 1 | 273.3 |
| 2 | 432.4 |
| 3 | 343.3 |
| 4 | 381.9 |
| 5 | 311.1 |
| 6 | 351.5 |
| 7 | 310.8 |
| 8 | 301.4 |
| 9 | 358.6 |
| 10 | 330.3 |
Tabla I: Medidas tomadas de la velocidad del sonido utilizando un tubo de Kundt en un laboratorio de física básica.
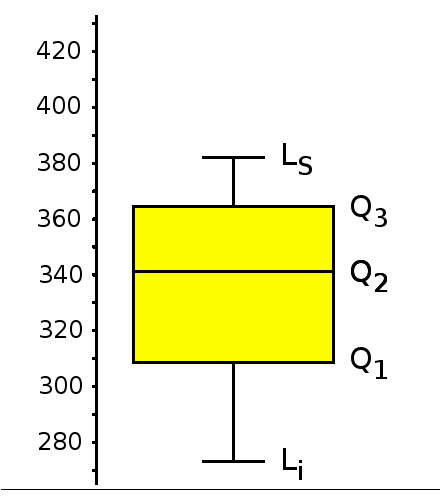
Diagrama de caja I: Representación de los datos de la tabla I.
El valor medio no necesariamente divide a la caja en partes iguales. Con un número de mediciones mas grande y dado que la velocidad del sonido es una magnitud física se esperaría que el valor medio divida la caja en partes iguales.
En el diagrama de caja I se representan los datos de la tabla. El diagrama consta de tres divisiones Q1, Q2 y Q3 llamadas cuartiles que definen la caja dividida. Por otro lado, los datos límites inferior Li y superior Ls definen la longitud de los brazos.
¿Qué son y cómo se obtienen lo cuartiles?
Los datos de la tabla se ordenan de menor a mayor y los cuartiles son tres valores que dividen a los datos en cuatro partes.
Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al 75% de los datos. Hay varias formas de calcular los cuartiles. Calculemos los cuartiles de la tabla I mediante una forma:
• Se ordenan los datos de menor a mayor
| 273.3 | 301.4 | 311.1 | 312.8 | 339.3 | 343.3 | 351.5 | 358.6 | 381.9 | 432.4 |
• Buscamos el lugar en la tabla ordenada que ocupa cada cuartil mediante la expresion k (N+1)/4. Con N igual al numero de datos y k el numero de cuartil (k=1,2 o 3).
En nuestro ejemplo el numero de datos es N=10
El primer cuartil esta ubicado en 1×11/4=2.75, es decir entre el segundo y tercer valor de la tabla.
El segundo cuartil esta ubicado en 2×11/4=5.5, es decir entre el quinto y sexto dato de la tabla.
El tercer cuartil esta ubicado en 3×11/4=8.25, es decir entre el quinto y sexto dato de la tabla.
| 273.3 | 301.4 | 311.1 | 312.8 | 339.3 | 343.3 | 351.5 | 358.6 | 381.9 | 432.4 |
| Q1=308.675 | Q2=341.3 | Q3=364.425 | |||||||
• Los cuartiles pueden coincidir con los valores de la tabla o no. Si no coinciden se hace una interpolación lineal utilizando la ubicacion del cuartil y los valores entre los cuales se encuentra. Así, en nuestro ejemplo:
Q1= 301.4 + 0.75*(311.1-301.4)=308.675
Q2= 343.3 + 0.5*(343.3-339.3)=341.3
Q3= 358.6 + 0.25*(381.9-358.6)=364.425
donde 0.75 para el primer cuartil se calculó como la resta de su posición en la tabla menos la parte entera de su posicion, es decir :1×11/4 -2=0.75. (Lo mismo para los otros cuartiles).
En http://www.alcula.com/es/calculadoras/estadistica/diagrama-de-caja/ puede construir su propio diagrama de caja que utiliza la forma de cálculo de los cuartiles explicada anteriormente.
Desventajas
🙁 Los diagramas de cajas no dan cuenta de las distribuciones reales asociadas a los datos estadísticos que representan. Por ejemplo si los datos provienen de una distribución gaussiana, uniforme, de Poisson, etc con un diagrama de cajas no podemos establecer el tipo de distribución. Razón por la cual no es utilizado en ciencias básicas como la física y la química.
Ventajas
🙂 Como herramienta de estadística descriptiva es sumamente útil debido a su fácil visualización
🙂 Se pueden representar más de una caja en un diagrama. Volviendo al ejemplo de medición de la velocidad del sonido (visto más arriba) se observa en el diagrama que sigue que se adicionaron cajas de la misma medición realizada en épocas diferentes del año. La velocidad del sonido depende de la temperatura ambiente.
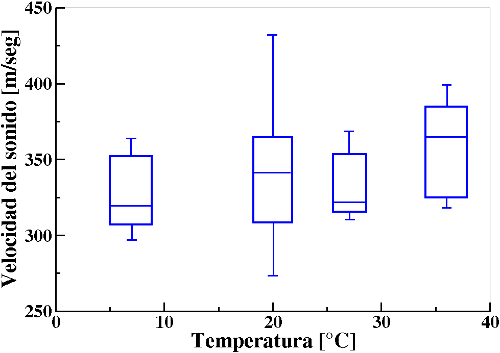
Diagrama de cajas II: Mediciones experimentales de la velocidad del sonido realizadas en diferentes épocas del año. Para cada caja se hicieron diez mediciones. La velocidad cambia con la temperatura ambiente.